PROF A Package for Respiratory Disease Open-source Forecasting
Welcome to the documentation site for the PROF package. PROF is an R package (with Fortran code) designed for fitting and forecasting infectious disease incidence. The package takes in either publicly-available confirmed hospital admission data, or user provided data, fits mechanistic and statistical models to the data, and provides short-term probabilistic forecasts. When incidence data is available for the forecasting time window, PROF uses the weighted interval score method to evaluate the accuracy of the probabilistic forecast.
Currently, the package supports fitting and forecasting the individual and combined burden of influenza and COVID-19 for single populations at any geographic scale. Susceptible-Infectious-Hospitalized-Recovered (SIRH) and Susceptible-Exposed-Infectious-Hospitalized-Recovered (SEIRH) models are employed to fit the two pathogens, and both models utilize a flexible, time-dependent transmission term. A baseline statistical model can also be used to fit and forecast each pathogen.
In the case of a mechanistic compartmental fitting, once the user selects a location (or uploads a hospitalization incidence file) and either one or both viruses, the PROF fitting procedure iteratively determines the joint posterior distribution of model parameters. This joint posterior distribution is then used with the compartmental model to generate location-specific probabilistic forecasts of the near-term number of hospital admissions.
If both viruses are chosen, this procedure is repeated, and the total hospital burden forecast is estimated by combining the trajectory profiles of each disease using an error correlation procedure. This procedure allows the user to tune the correlation between the errors of the individual forecasts when estimating the combined burden.
In the case of a baseline statistical model, the user can also select to fit (or forecast) either both pathogens or only one of them. This simple model is fast but its informative value is limited to early/late times in the season when changes in the incidence are small.
The PROF computational engine is complemented with a user-friendly GUI. We recommend using the GUI in all cases, except when fitting and forecasting multiple locations sequentially.
Data
PROF provides full support for downloading the most up-to-date daily, or weekly, confirmed hospital admission data for COVID-19 and influenza. Within the PROF-shiny GitHub we provide a recent data set to enable immediate use of the package. If we estimate that there is newer data we provide a download option and prompt the user to use it.
The data set is provided by the U.S. Department of Health & Human Services, is updated weekly on Friday, and is called: "COVID-19 Reported Patient Impact and Hospital Capacity by State (RAW)". For more on the data set, see here.
Note: As of May 3, 2024 this dataset has not been updated because hospitals are no longer required to report data on COVID-19 hospital admissions to HHS through the CDC's National Healthcare Safety Network (NHSN). Data reported voluntarily to NHSN after May 1 is available at COVID Data Tracker Hospitalizations. Once mandatory reporting resumes, PROF will resume its automatic data update procedure.
PROF also provides support for user uploaded data. The data can be either daily or weekly and it must follow certain specifications. See PROF-Advanced Topics/Uploading Your Own Data for more details.
Compartmental Models
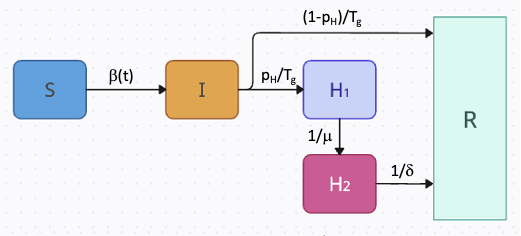
PROF uses compartmental models with a flexible, time-dependent transmission term to fit daily or weekly hospitalization data. Whereas pathogen can be fitted by either one of the models we support, we do recommend using the SEIRH model for COVID-19 and the SIRH model for influenza. Both models include a hospitalization compartment which is split into two sub-compartments. This split ensures that the model preserves the correct generation time (Tg) and that the ratio between cumulative recovered and hospitalized individuals is determined by the infection-hospitalization-ratio (pH). In the SIRH mode, individuals begin in the susceptible compartment. If exposed, they transition (β(t)) to the infectious compartment where there is a probability of hospitalization or recovery (pH or 1-pH) Individuals progress (1/μ) from the first hospitalization compartment (H1) to the second (H2), and the number entering this compartment is recorded as daily (or weekly) incidence (and optimized, see below).
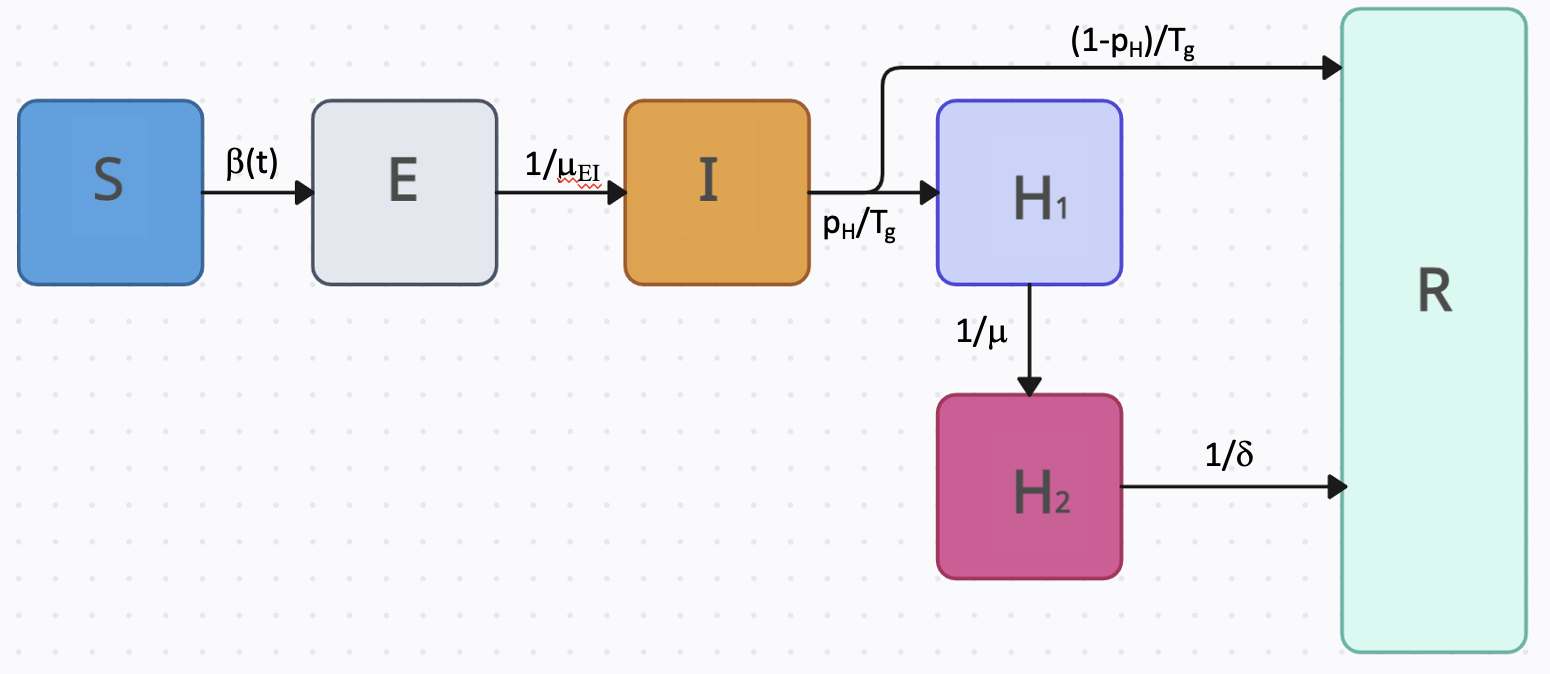
The SEIRH model is similar with the only difference being the addition of the Exposed (but not yet infectious) compartment.
While we recommend utilizing the SIRH model for influenza and SEIRH for COVID-19, PROF is flexible and supports the fitting of either model to either pathogen.
PROF fits each pathogen independently and sequentially. For each pathogen, we determine the joint posterior distribution of model parameters by fitting the daily (or weekly) confirmed hospital admission time series using an adaptive-step-size MCMC procedure. Only parameters that govern the time variation of R(t) and the probability of hospitalization are optimized and all other parameters are taken from the literature. A fast Fortran code is used for the MCMC procedure. Once the fitting of one pathogen is completed, PROF proceeds to fit the second pathogen. The posterior distribution of each fit can be used to (1) Create a probabilistic plot of the fit, (2) Create a probabilistic forecast (and plot thereof) for each pathogen.
Time-Dependent Force of Infection
We use a smoothly varying two- or three-value functional form to describe the time-dependent reproduction number: R(t) = β(t)γ, where β(t) is the time-dependent transmission rate and γ is the total recovery rate.
$$R(t)=\frac{1}{2}\left( R_{0} + R_{1} + (R_{1}-R_{0})tanh\left( \frac{t-t_{0}}{L} \right) \right)$$
The above equation is for the case of a two-value R(t). It produces a smooth curve where at roughly time t0 the value of R(t) transitions from R0 to R1 with an approximate transition time of \~2L days. For the general case of three (or more) values see Ben-Nun et al. 2022
Baseline Statistical Model
In addition to fitting and forecasting the data with a compartmental model PROF can fit and forecast the data to a baseline statistical model. For weekly data, the median prediction of the baseline forecast is the corresponding target value observed in the previous week, and noise around the median prediction is generated using positive and negative 1-week differences (that is differences between consecutive reports) for all prior observations. The resulting sampling distribution is truncated to prevent negative values. PROF implements this model using daily (or weekly) data and uses it to sequentially fit and forecast the data.
The combined burden of the Statistical forecast is evaluated using the same error-correlation procedure as described above.
Estimating the Combined Burden of Multiple Pathogens
The final step in PROF involves providing an estimation for the forecast of the combined burden. The uncertainty associated with this combined burden is determined through our error-correlation procedure. Essentially, this procedure introduces a tunable parameter (with a range from zero to one) that adjusts the combination of uncertainties present in the individual forecasts. A value of one indicates full correlation among the individual errors, leading to greater uncertainty in the combined forecast. Conversely, a value of zero suggests errors that are entirely independent, resulting in a narrower forecast.
By default, PROF calculates the combined burden using values of zero and one. The user is prompted to adjust the default value of one to any value in the 0-1 range. Consequently, two combined burden estimates are provided: one assuming a correlation between the errors, as set by the user, and another assuming no correlation between the errors of the two forecasts.
The combined burden estimates are available for both compartmental and statistical models and require the fitting and forecasting of both pathogens.
Mixing Compartmental and Statistical Forecasts
As explained in the Advanced Topics Section, the command-line version of PROF provides an option to create a mixed forecast by combining mechanistic and statistical forecasts with equal weights.