Graph Analysis

The following section will analyze the results of the tracking algorithm on the time interval of 100 days from December 29th, 2010 to April 8th, 2011 (with 2 hr cadence).

Graph Results

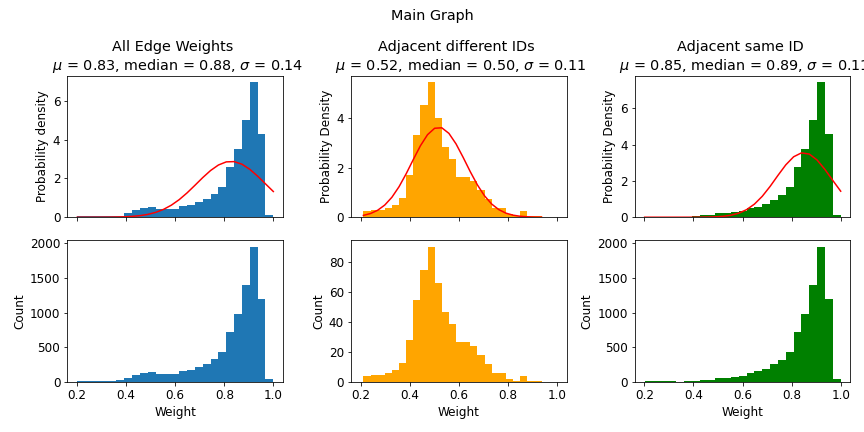
• Total number of nodes:  8467
• Total number of edges:  8742
• Number of edges between nodes of the same ID: 8172
• Number of edges between nodes with different ID: 570
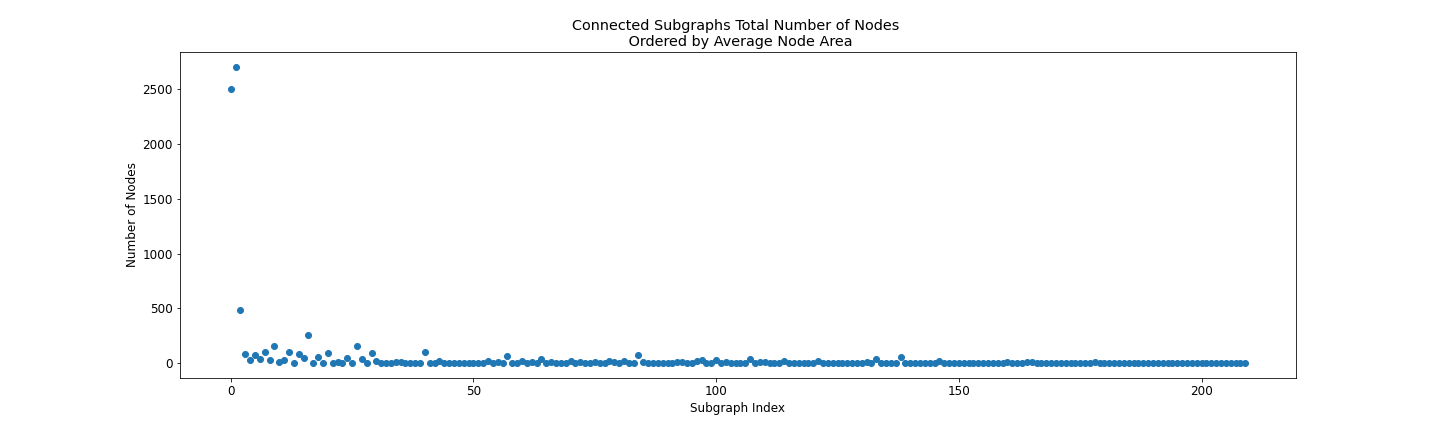
• Total number of subplots:  210

Graph Traversal

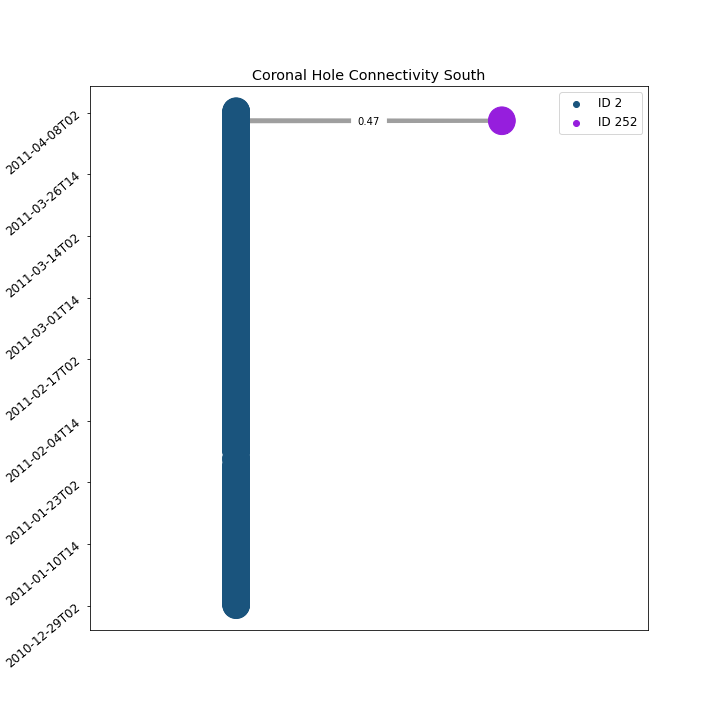
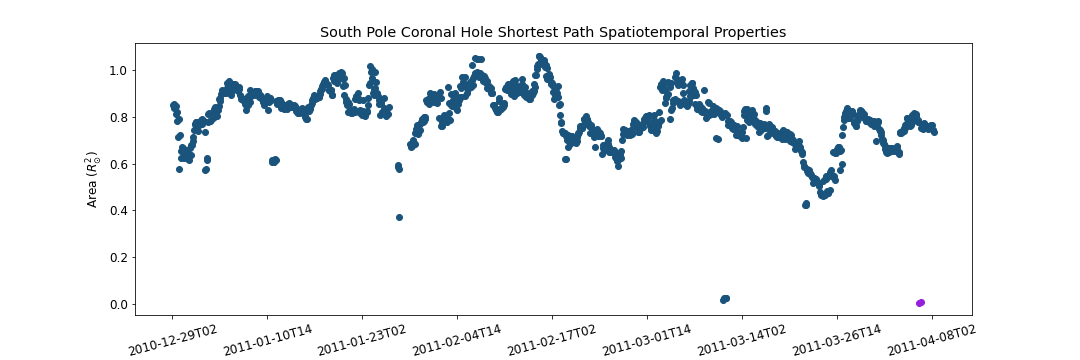
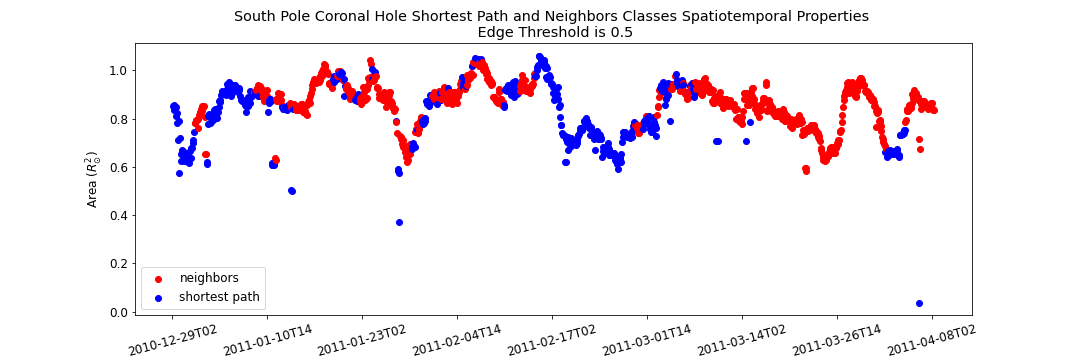
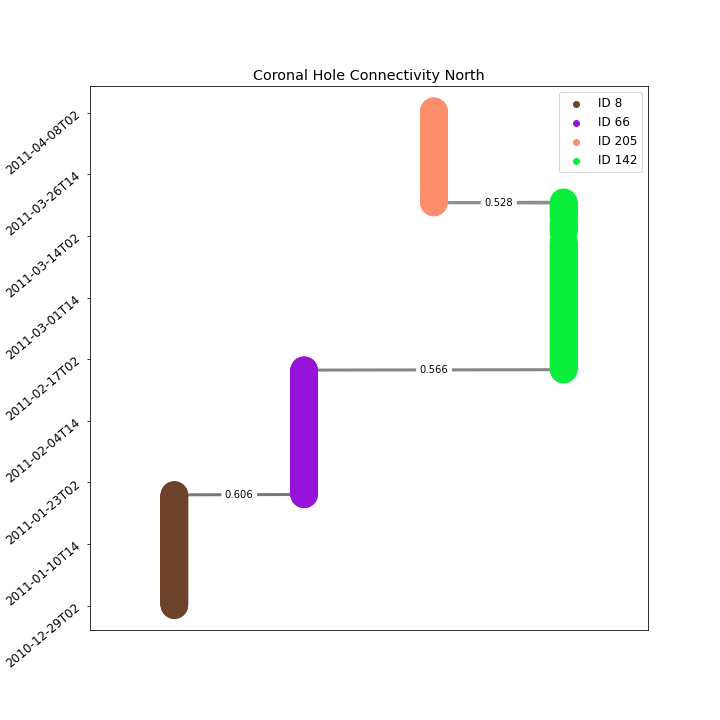
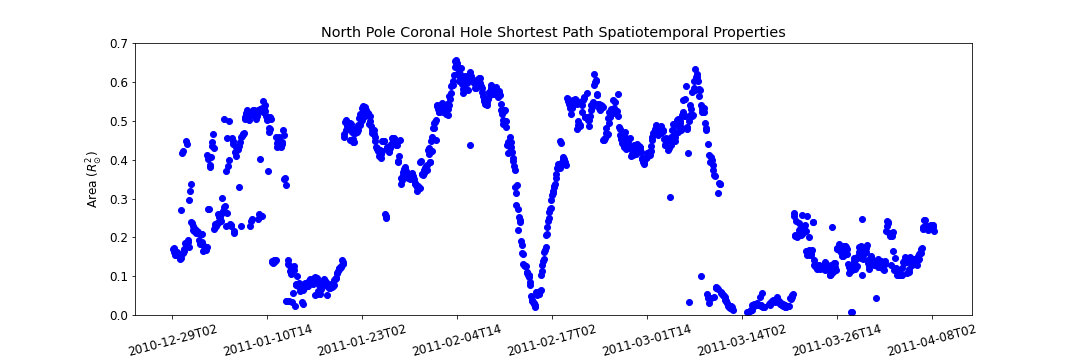
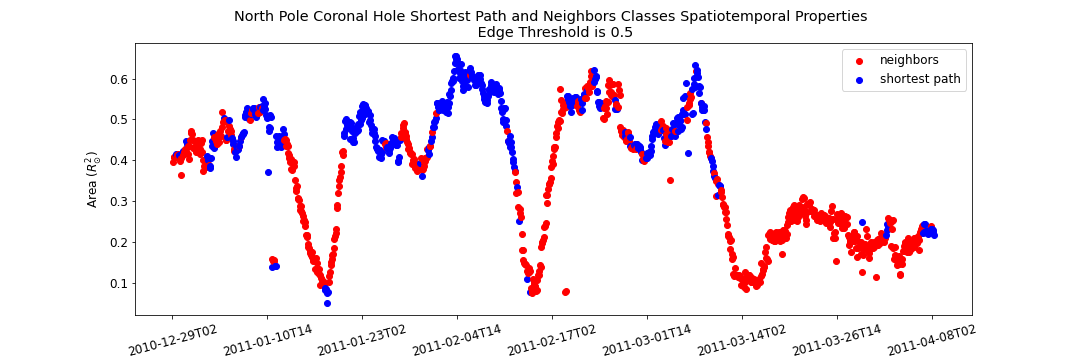
Graph Traversal refers to the process of searching each edge in a graph. How can we find the optimal path that will represent the spacial temporal evolution of a given coronal hole? We can think about traversing the coronal hole connectivity graph as a variant of the "traveling salesman problem", where the goal is to find the shortest path between two nodes in a finite graph. Here we leverage Dijkstra's shortest path Algorithm to find the optimal path. The cost function used to set up the minimization problem is as follows

$$COST(n_{1}, n_{2}) = \begin{array}{cc} \{ & \begin{array}{cc} 0 & n_{1}.id = n_{2}.id \\ 1 - w(n_{1}, n_{2}) & n_{1}.id \neq n_{2}.id \end{array} \} \end{array}$$

Where $n_{1}, n_{2}$ are two arbitrary nodes and $w(n_{1}, n_{2})$ is the edge weight between the two nodes. Such cost function will minimize the number of explored classes, and enforce the route of more long-lasting coronal holes. Also, such cost function will favor the paths with stronger area overlap association.

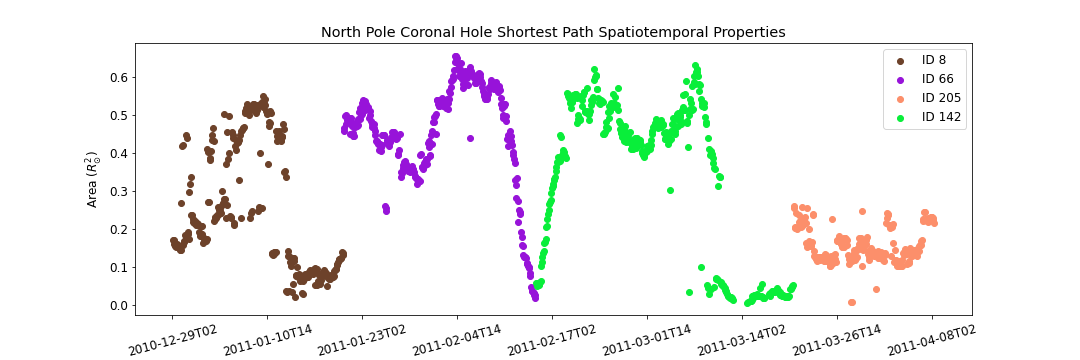
North Pole Coronal Hole Evolution

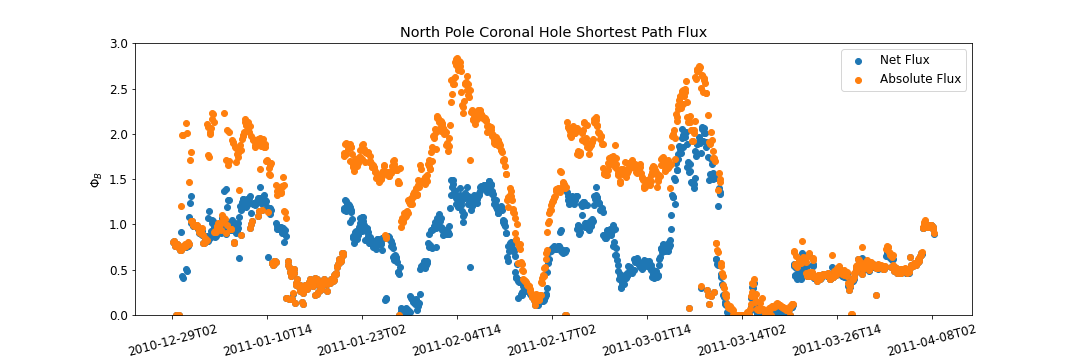
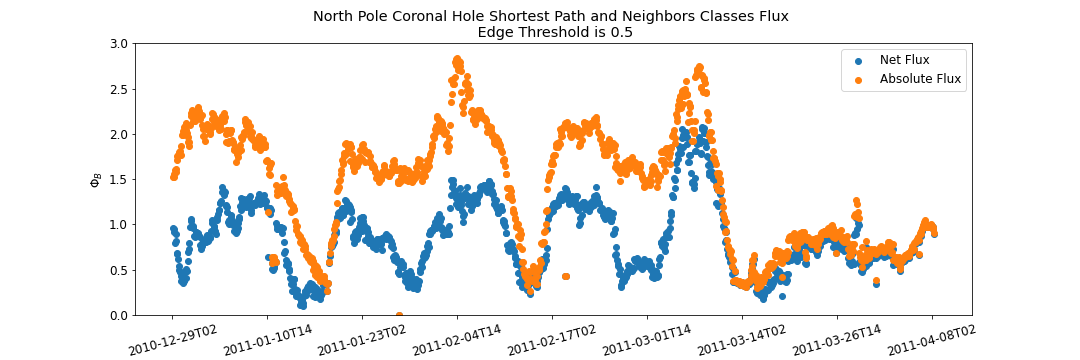
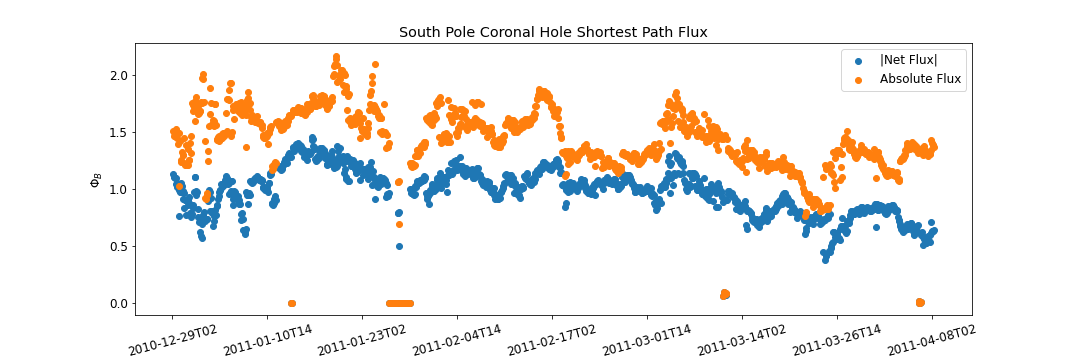
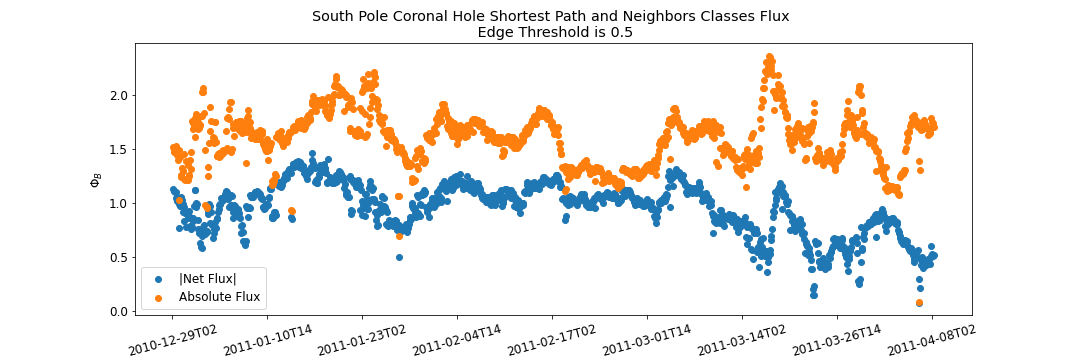
South Pole Coronal Hole Evolution